当ブログはプロモーションを含みます
図書館でこんな本を借りてみました。
『小学校6年分の算数が教えられるほどよくわかる なぜ?を解決!』
分数の割り算では、なぜひっくり返してかけるの?
園の面積はなぜ「半径×半径×円周率」で求まるの?
など、算数のなぜ?を解決する本です。
私が今まで算数を勉強してきて全く疑問に思わなかったことばかりが掲載されているんですけど、読んでみると今更ながらに「なるほどね!!」と思うことが多くて面白い!
全部は読んでいなくて、興味があるところと1年生のところを読んでみたんですけど、1年生の算数の山場である「さくらんぼ計算」についても書かれていて、これがなかなか奥が深いことが分かりました。
例えば繰り上がりのある足し算の場合。
8 + 6 = 14
この計算をさくらんぼ算でする時、
まず、8にいくつ足したら10になるか⇒2
次に、6は2といくつ?⇒4
最後に10と4を足したら?⇒14
と計算するじゃないですか。
この本ではないけれど、ネットで検索していた時に、分解するのは小さい数の方だ!と書かれていたんですよ。だから「4+7」の場合は、4の方を分解する、みたいな。
まぁ、足し算はいいんですよ。
問題は引き算。
繰り下がりのある引き算のさくらんぼ算には2種類あるそうな。
1つ目が「引いてたすさくらんぼ計算」。
私のつたない図解で失礼します。。。
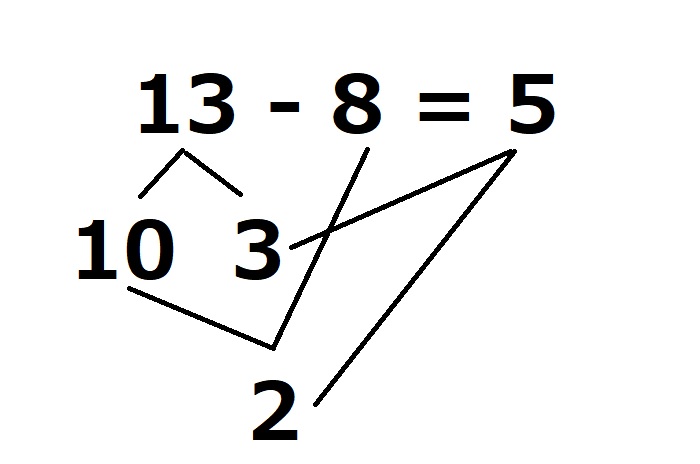
「13-8=5」を計算するとき、「13を10と3に分解」して「10-8=2」を計算した後、「3+2=5」と計算するんですって・・・いや、これは小学1年生に理解できるのか?私でもちょっとややこしい。
そこで2つ目の「引いて引くさくらんぼ計算」。
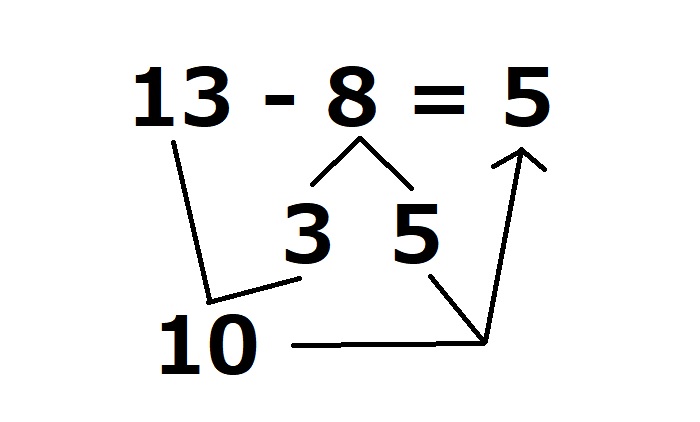
「13-8=5」を計算するとき、「8を3と5に分解」して「13-3=10」を計算した後、「10-5=5」と計算するそうです。うん、こっちの方が「引き算」って分かりやすい。
この2パターンがある、ってこの本を読んで初めて知りました。
小学校の算数(下)の教科書が手元にないので、学校ではどうやって教えるのか分かりませんが、夏休みに「さくらんぼ算」の予習をした場合、「引いて引くさくらんぼ計算」で教えようと思います。
この本にもシッカリ書いてありました。
「たして10になる数」をスムーズに言えるようになる必要があります、と。
やっぱり「10を制するものが繰り上がり・繰り下がりを制す」のね。
息子はだいぶ、いくつといくつ名人になってきたので、免許皆伝を目指そうと思います。
子供が大きくなったときに算数の疑問にパパッと答えられたら尊敬されるだろうな、という妄想ができちゃう本です。賢い5,6年生の場合は子供自身に読ませると算数の世界を面白く感じられるかもしれないな。























この記事へのコメントはありません。